Winddreieck

Beschreibung:

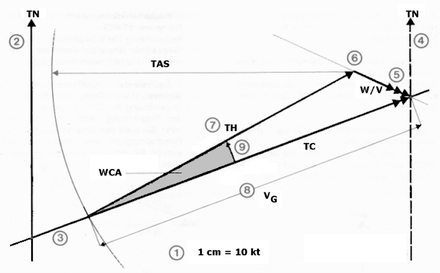
Das Winddreieck ist eine Methode in der Luftfahrtnavigation, die grafisch zeigt, wie der Wind Richtung und Geschwindigkeit eines Flugzeugs beeinflusst. In der Schifffahrt wird eine ähnliche Technik verwendet, um zu bestimmen, wie Strömungen den Kurs beeinflussen.

Voraussetzungen für die Erstellung eines Winddreiecks

Sechs spezifische Werte definieren Form und Position des Winddreiecks, das entweder durch Berechnungen oder grafische Darstellungen ermittelt werden kann, sofern vier dieser sechs Werte bekannt sind.

Die Kurse und Geschwindigkeiten

Die Werte Winddreiecks immer ein Kurs mit einer Geschwindigkeit:

1. Rechtweisender Steuerkurs (rwSK, TH - True Heading) und Fahrt (TAS - True Airspeed):

   • Der rechtweisende Steuerkurs (TH) ist der Kurs, den das Fahrzeug (z. B. ein Flugzeug) relativ zum geografischen Nordpol steuert. Die Fahrt (TAS) ist die Geschwindigkeit des Fahrzeugs relativ zur umgebenden Luft. Zusammen geben diese beiden Werte an, wie sich das Flugzeug durch die Luft bewegt, unabhängig von externen Einflüssen wie Wind.

2. Rechtweisender Kurs (rwK, TC - True Course) und Geschwindigkeit über Grund (VG, GS - Ground Speed):

   • Der rechtweisende Kurs (TC) ist die tatsächliche Richtung, in die sich das Fahrzeug über den Boden bewegt, und die Geschwindigkeit über Grund (GS) ist die Geschwindigkeit des Fahrzeugs relativ zum Boden. Diese beiden Werte werden durch den Einfluss des Windes auf das Fahrzeug beeinflusst. Der Wind kann die tatsächliche Bewegung über den Boden verändern, indem er das Fahrzeug seitlich versetzt oder seine Vorwärtsbewegung beeinflusst.

3. Windrichtung (TWD - True Wind Direction) und Windgeschwindigkeit (VW, WS - Wind Speed):

   • Die Windrichtung (TWD) gibt an, aus welcher Richtung der Wind weht, und die Windgeschwindigkeit (WS) ist die Geschwindigkeit dieses Windes. Diese Informationen sind entscheidend, um zu berechnen, wie der Wind den Kurs und die Geschwindigkeit des Fahrzeugs beeinflusst.

4. Luvwinkel (WCA - Wind Correction Angle):

   • Der Luvwinkel ist der Winkel, der benötigt wird, um den Einfluss des Windes auszugleichen, damit das Fahrzeug seinen gewünschten Kurs über Grund (TC) beibehalten kann. Er ergibt sich aus der Differenz zwischen dem rechtweisenden Steuerkurs (TH) und dem rechtweisenden Kurs (TC). Dieser Winkel ist notwendig, um den Seiteneffekt des Windes auszugleichen und die geplante Richtung beizubehalten.

Zusammenfassend lässt sich sagen, dass die Kombination dieser Kurse und Geschwindigkeiten es Navigatoren ermöglicht, die genaue Bewegung und Ausrichtung eines Fahrzeugs in Relation zu Windbedingungen zu bestimmen und entsprechende Korrekturen vorzunehmen, um die gewünschte Route effektiv zu navigieren.

Zeichnen des Winddreickes

Materialien:

• Papier
• Bleistift
• Lineal oder Geodreieck
• Kompass oder ein Winkelmesser

Schritte zur Konstruktion des Winddreiecks:

Norden ist immer oben, wie auf Karten. Das vereinfacht das ganze.
1cm = 10 KT

1. Zeichne den rechtweisenden Kurs (True Course, TC):

   • Beginne mit dem Zeichnen einer Linie vom Punkt A (Startpunkt) nach Punkt B. Diese Linie stellt den rechtweisenden Kurs (TC) dar, also die Richtung, in die das Fahrzeug tatsächlich über den Boden navigieren soll. Die Länge dieser Linie kann proportional zur Geschwindigkeit über Grund sein, kann aber auch zunächst als eine Einheitslänge betrachtet werden.

2. Markiere die Windrichtung und -geschwindigkeit:

   • Vom Startpunkt A aus zeichnest du eine zweite Linie, die die Windrichtung (TWD) anzeigt. Der Winkel dieser Linie zum rechtweisenden Kurs entspricht der Windrichtung, und die Länge dieser Linie entspricht der Windgeschwindigkeit (WS). Dies ist der Vektor des Windes.

3. Füge die wahre Fahrtgeschwindigkeit (True Airspeed, TAS) hinzu:

   • Vom Ende der Windrichtungslinie (Punkt C, das Ende des Windvektors) ziehe eine Linie zurück zum Punkt B. Diese Linie repräsentiert die wahre Fahrtgeschwindigkeit (TAS) des Flugzeugs. Sie sollte so angelegt werden, dass, wenn du die Vektoren in Bezug auf Größe und Richtung korrekt gezeichnet hast, die resultierende Linie von Punkt C nach Punkt B zeigt.

4. Ermittle den Luvwinkel (WCA):

   • Der Winkel zwischen der Linie des rechtweisenden Kurses (AB) und der Linie des rechtweisenden Steuerkurses (AC) ist der Luvwinkel (WCA). Dieser Winkel ist notwendig, um den rechtweisenden Steuerkurs (TH) zu bestimmen, der benötigt wird, um den Wind zu kompensieren.

5. Bewertung der Geschwindigkeit über Grund:

   • Die Länge der Linie von A nach B kann nun gemessen werden, um die Geschwindigkeit über Grund (GS) zu bewerten, wenn die Skalierung der Linien entsprechend der Geschwindigkeiten angepasst wurde.

Tipps:

• Benutze für genaue Winkel und Linienlängen ein Geodreieck und einen Winkelmesser.
• Es kann hilfreich sein, unterschiedliche Farben für die verschiedenen Linien zu verwenden, um die Übersicht zu behalten.

Bild Quelle Wikipedia

Rechnerisch ermitteln

Stell dir vor, du hast ein Dreieck gezeichnet, und jede Seite des Dreiecks ist ein Stück einer Reise:

1. Eine Seite ist, wie schnell das Flugzeug durch die Luft fliegt (das nennen wir True Airspeed, TAS).
2. Eine andere Seite zeigt, wie schnell das Flugzeug tatsächlich über den Boden bewegt (das nennen wir Ground Speed, GS).
3. Die dritte Seite ist der Wind, der das Flugzeug schiebt oder zieht (das nennen wir Wind Speed, WS).

Nun, wir wollen herausfinden, wie wir das Flugzeug lenken müssen, damit es genau dort ankommt, wo wir es haben wollen, auch wenn der Wind versucht, es anderswohin zu schieben. Wir nutzen dafür etwas, das heißt Sinussatz, der uns hilft, die Längen der Seiten oder die Größe der Winkel in unserem Dreieck zu finden, wenn wir schon ein paar von ihnen wissen.

So funktioniert der Sinussatz:

• Der Sinussatz sagt uns, dass das Verhältnis zwischen einer Seite des Dreiecks und dem Sinus (das ist eine mathematische Funktion, die den Winkel misst) des gegenüberliegenden Winkels für alle drei Seiten gleich ist.

Beispiel:

Wenn du weißt, wie stark der Wind ist (WS) und wie schnell das Flugzeug über den Boden gehen soll (GS), und du den Winkel kennst, den der Wind zum Flugzeug macht, kannst du herausfinden:

• Wie schnell das Flugzeug durch die Luft gehen muss, um gegen den Wind anzukommen.

Einfache Erklärung:

Stell dir vor, du willst geradeaus über einen Fluss schwimmen, aber die Strömung will dich zur Seite schieben. Du musst ein bisschen schräg schwimmen, um genau gegenüber anzukommen, wo du hinwillst. Der Sinussatz hilft dir herauszufinden, wie schräg du schwimmen musst, um trotz der Strömung dein Ziel zu erreichen.

Berechnungsbeispiel:

Gegeben:

• GS (Geschwindigkeit über Grund) = 100 KT
• TC (rechtweisender Kurs) = 200°
• WS (Windgeschwindigkeit) = 10 KT
• TWD (Windrichtung) = 110°

Ziel:

• Berechnung von TAS (wahre Fahrtgeschwindigkeit)
• Berechnung von TH (rechtweisender Steuerkurs)
• Berechnung von A (Wind Correction Angle)
  

Schritte zur Lösung:

1. Bestimme den Winkel zwischen der Windrichtung und dem Kurs über Grund (relativer Windwinkel):

   Relativer Windwinkel  : TC−TWD=Relativer Windwinkel
   Relativer Windwinkel : 200°−110°=90°
   
   

2. Anwendung des Kosinussatzes zur Berechnung von TAS:
   Der Kosinussatz lautet:

   c²=a²+b²−²ab⋅cos⁡(C)

   Hierbei ist:

   • $c=TAS$
   • $a=GS$
   • $b=WS$
   • C=Relativer Windwinkel=90°

   Setze die Werte ein:
   
   TAS²=100²+10²−2⋅100⋅10⋅cos(90°)
   Hier ist zufällig COS(90°) = 0
   Also ist dann nur noch
   TAS²=100²+10²−2⋅100⋅10
   TAS²=10000+100=10100
   
   nun die Wurzel aus 10100 ​≈100.5 KT

3. $$\text{Anwendung des Sinussatzes zur Berechnung von TH: WS = Windgeschwindigkeit waren hier 10 KTDen Windwinkel haben wir ja als erstes berechnet die waren 90 °}$$

   

   $$\text{Da A (WCA) der Winkel ist, um den der wahre Kurs (TC) korrigiert werden muss, ergibt sich für TH: Also 5,7 Grad addieren zu 200 °}$$$$\text{TH=TC+ATH=200°+5.7°=205.7°}$$

   Ergebnis:

   • TAS ≈ 100.5 KT
   • WCA = 5,7°
   • TH ≈ 205.7°

   Dieses Beispiel zeigt, wie der Wind, der quer zum Kurs bläst, sowohl die wahre Fahrtgeschwindigkeit geringfügig erhöht als auch eine kleine Korrektur des Steuerkurses erfordert, um den gewünschten Kurs über Grund beizubehalten.